Rainbows are one of nature’s most spectacular phenomena, serving as a bridge between the science of light and the artistry of colors. Often seen as a symbol of hope and inspiration, rainbows have also captivated mathematicians and educators, leading to interesting explorations into ‘rainbow numbers’ – a concept that adds a colorful twist to learning mathematical concepts. In this article, we’ll delve into some fascinating rainbow number facts and explore how students can apply this knowledge in their academic pursuits.
The magic of rainbows starts with sunlight and raindrops. When light passes through a raindrop, it bends in a process called refraction. This bending causes the light to spread out into its various colors, creating the spectrum we know as a rainbow. The order of colors is always the same: red, orange, yellow, green, blue, indigo, and violet, an array that can be remembered by the acronym ROYGBIV.
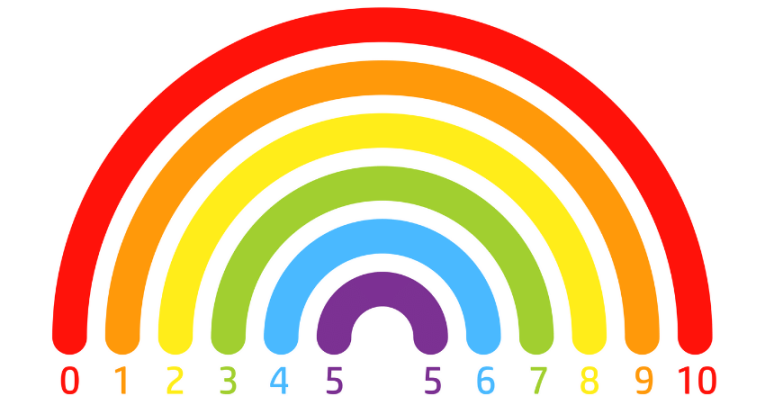
But beyond their visual beauty, rainbows have inspired educators to develop the concept of rainbow numbers for teaching addition in an engaging way. Rainbow numbers are pairs of numbers that combine to make certain totals. These pairs can be visualized just like the bands of color coming together to form a rainbow.
For example, consider the number 10. Some rainbow number pairs for 10 would be (1,9), (2,8), (3,7), and (4,6). By understanding these pairs, students can strengthen their mental arithmetic skills and develop a stronger grasp of addition and subtraction.
Moreover, the application doesn’t stop with primary education. For secondary students studying algebra and beyond, the visual model of ‘combining pairs’ helps with understanding inverse operations and balance within equations. Students can imagine adding x and y to reach across their own equation ‘rainbows’, seeing at a glance how different values interact to form solutions.
The concept further expands into areas such as statistics. Here, ‘rainbow numbers’ might manifest as data sets that are symmetric around a central point – much like how colors are distributed across a rainbow’s arch. Understanding symmetry in data sets can help students analyze balance in distribution patterns which is crucial while learning about means, medians, and modes.
Interdisciplinary projects also benefit from this colorful concept. For instance, students can collaborate on creating artistic representations of mathematical principles based on rainbow structures or engage in scientific experiments explaining light refraction while simultaneously employing mathematical concepts to quantify their observations.
Rainbow number facts provide more than just trivial tidbits; they’re bridges connecting mathematical thought with tangible reality. When students learn how to find harmony between numbers just as nature finds balance within a spectrum of light hues – they don’t just solve problems on paper; they’re prepared to look for solutions in multidimensional spaces abounding with color and creativity.
As educators incorporate these engaging concepts into curriculums worldwide, they’re not only teaching computation; they’re fostering the innate human capacity for seeing connections through diverse lenses – be it scientific or artistic. Students who embrace these principles may find themselves at the end of their educational rainbows not just reaching for pots of gold but building them brick by golden brick with knowledge attained along their chromatic journey.